Ανάλυση σε συνιστώσες

Είναι η αντίστροφη διαδικασία της σύνθεσης δυο δυνάμεων. Σκοπός είναι να βρούμε τις συνιστώσες, όταν μας δίνεται η συνισταμένη. Συνήθως η ανάλυση γίνεται πάνω σε δυο κάθετους άξονες.

Για να αναλύσουμε μια δύναμη σε συνιστώσες ακολουθούμε την εξής διαδικασία:

• Επιλέγουμε τους κάθετους άξονες x και y.
• Προβάλουμε το διάνυσμα της δύναμης σε κάθε έναν από τους άξονες.
• Σχηματίζουμε τις συνιστώσες της συνισταμένης δύναμης σε κάθε έναν από τους άξονες.
• Υπολογίζουμε τα μέτρα των συνιστωσών από τις σχέσεις:

Τρέξτε την προσομοίωση:

Πατήστε εκκίνηση και παρατηρήστε ποια είναι η διαδικασία ανάλυσης μιας δύναμης.

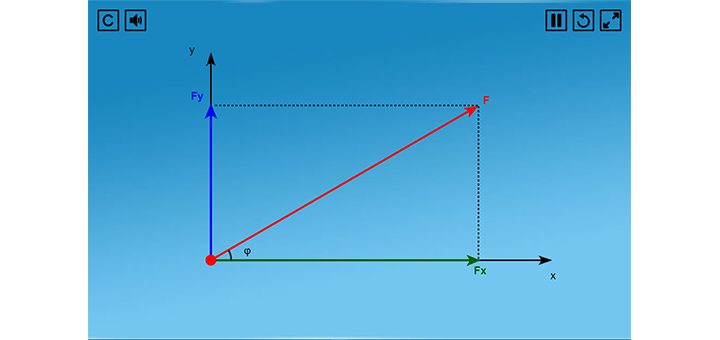
Η περίπτωση της ανάλυσης του βάρους σε κεκλιμένο επίπεδο.

Για να αναλύσουμε το βάρος σε συνιστώσες, ακολουθούμε μια ανάλογη της προηγούμενης διαδικασία.

Τρέξτε την προσομοίωση:

Με τη βοήθεια της μπάρας επιλέξτε τη γωνία του κεκλιμένου επιπέδου. Πατήστε εκκίνηση και παρατηρήστε πως σχηματίζονται οι συνιστώσες $w_x$ και $w_y$ της δύναμης του βάρους.

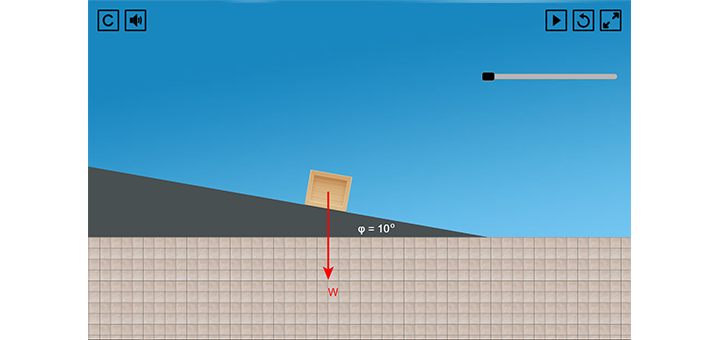
Προσπαθήστε να απαντήσετε στις παρακάτω ερωτήσεις:

Προσομοίωση 1:

Στην περίπτωση που η γωνία μεταξύ της συνισταμένης δύναμης $F$ και του οριζόντιου άξονα είναι $30°$:

1. Ποια είναι η τιμή της συνιστώσας $F_x$;
2. Ποια είναι η τιμή της συνιστώσας $F_y$;

Δίνονται: $F=10N$, $ημ30°=1/2$ και $συν30°=?3/2$

Προσομοίωση 2:

Στην περίπτωση που η γωνία του κεκλιμένου επιπέδου είναι $30°$ και η μάζα του σώματος $m=2kg$:

1. Πόσο είναι το βάρος $w$ του σώματος;
2. Ποια είναι η τιμή της συνιστώσας $w_x$;
3. Ποια είναι η τιμή της συνιστώσας $w_y$;

Δίνονται: $g=10 m/s^2$