Σύνθεση δυνάμεων στο επίπεδο

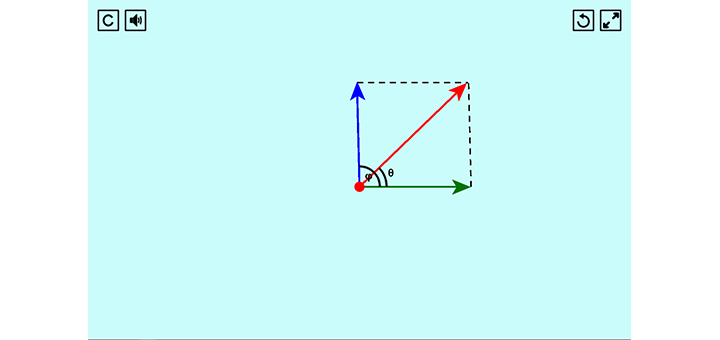
Για να υπολογίσουμε τη συνισταμένη δυο δυνάμεων $F_1$ και $F_2$ στο επίπεδο, ακολουθούμε την εξής διαδικασία:

Φέρνουμε από το άκρο της $F_1$ παράλληλη στην $F_2$ , ομοίως από το άκρο της $F_2$ παράλληλη στην $F_1$. Η διαγώνιος αυτού του παραλληλογράμου είναι η $F_{ολ}$.

Το μέτρο αυτού του διανύσματος είναι ίσο με:

$$F_{ολ}=?{F_1^2+F_2^2+2·F_1·F_2·συνφ}$$

και η κατεύθυνση: $$εφθ={F_2·ημφ}/{F_1+F_2·συνφ}$$

Τρέξτε την προσομοίωση:

Σύρετε με το δάκτυλο την μπλε και πράσινη δύναμη για να καθορίσετε τις συνιστώσες. Πατήστε το κουμπί της εκκίνησης για να δείτε τη διαδικασία εύρεσης της συνισταμένης.

• Η περίπτωση των κάθετων δυνάμεων:

Για να υπολογίσουμε τη συνισταμένη δυο κάθετων δυνάμεων, ακολουθούμε μια διαδικασία παρόμοια με την προηγούμενη και υπολογίζουμε το μέτρο και την κατεύθυνση της συνισταμένης, με τη βοήθεια των σχέσεων: $$F=?{F_1^2+F_2^2}$$ και $$εφθ=F_2/F_1$$

• Προσπαθήστε να απαντήσετε στις παρακάτω ερωτήσεις:

Δίνονται οι δυο κάθετες δυνάμεις, $$F_1=8N$$ και $$F_2=6N$$. Να υπολογίσετε:

1. Τη συνισταμένη δύναμη $F_{ολ}$
2. Την κατεύθυνση της συνισταμένης δύναμης.