Οριζόντια βολή
Οριζόντια βολή, είναι η κίνηση που εκτελεί ένα σώμα μάζας $m$ όταν εκτοξεύεται με οριζόντια αρχική ταχύτητα $u_0$ και κινείται μόνο με την επίδραση του βάρους του. Είναι σύνθετη κίνηση και αποτελείται από μια ευθύγραμμη ομαλή και μια ελεύθερη πτώση.
Στην οριζόντια βολή ισχύει η αρχή ανεξαρτησίας των κινήσεων: η κάθε κίνηση εξελίσσεται ανεξάρτητα από την άλλη, ενώ ο χρόνος είναι κοινός στις δύο κινήσεις.
Αναλυτικά:
Άξονας x: Ευθύγραμμη ομαλή κίνηση με εξίσωση:
Άξονας y : Ελεύθερη πτώση με εξισώσεις:
και
Η τροχιά της οριζόντιας βολής είναι μια παραβολή.
Σε κάθε θέση της κίνησης του σώματος η ταχύτητά του δίνεται από τη σχέση:
και
Τρέξτε την προσομοίωση:
Με τις οριζόντιες μπάρες μπορείτε να ρυθμίσετε το ύψος και την αρχική ταχύτητα, ενώ από τις ρυθμίσεις ποια μεγέθη θα εμφανίζονται.
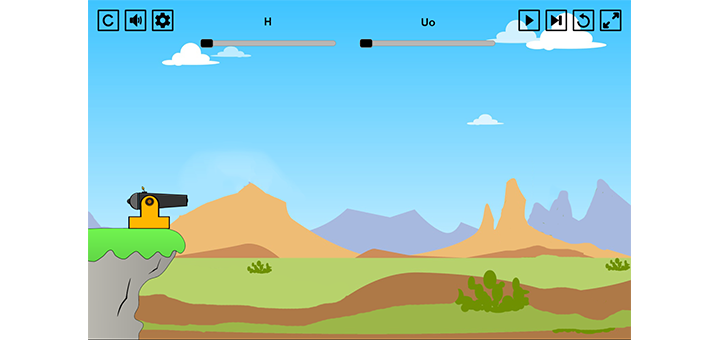
Προσπαθήστε να απαντήσετε στις παρακάτω ερωτήσεις:
Το βλήμα της προσομοίωσης εκτοξεύεται με αρχική ταχύτητα $u_0=30m/s$ και από ύψος $H=80m$.
- Σε πόσο χρόνο $t$ θα χτυπήσει στο έδαφος;
- Πόση θα είναι η μέγιστη οριζόντια μετατόπισή του (βεληνεκές);
- Με τι κατακόρυφη ταχύτητα θα χτυπήσει στο έδαφος;
- Με τι ταχύτητα θα χτυπήσει στο έδαφος;
- Πόσο θα απέχει από το έδαφος, $2s$ μετά τη στιγμή της εκτόξευσής του;
Δίνεται: $g=10m/s^2$
- Από τη σχέση: $y=1/2·g·t^2$, για $y=H$, έχουμε: $t=?{2·H/g}?t=?{2·80/10}?t=4s$
- $x=υ_0·t?x=30·4?x=120m$
- $u_y=g·t?u_y=10·4?u_y=40m/s$
- $u=?{u_0^2+u_y^2}?u=?{30^2+40^2}?u=50m/s$
- Σε χρόνο $t=2s$ θα πέσει κατά $y=1/2·g·t^2?y=1/2·10·2^2?y=20m$, οπότε: $h=H-y?h=80-20?h=60m$



Πρόσφατα σχόλια